Final answer:
After calculating daily increases for Purses A and B over several time frames, it's evident that Purse B, which doubles its amount every day, holds a vastly greater sum after 30 days, illustrating the power of compound interest.
Step-by-step explanation:
Calculating Growth in Purses A and B
Let's start by determining the amount in each purse after one week (7 days) and after two weeks (14 days). Purse A gains $200 more each day, starting with $1,000 on day 1. Purse B's amount doubles every day, beginning with 1 penny on day 1.
For Purse A, we can calculate the total after one week as:
$1,000 + (6 days × $200/day) = $1,000 + $1,200 = $2,200
After two weeks (14 days):
$1,000 + (13 days × $200/day) = $1,000 + $2,600 = $3,600
For Purse B, since the amount doubles each day, we use the power of 2 to represent the growth:
After one week (7 days):
1 penny ×
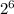 = 64 pennies (because we don't count the first day)
= 64 pennies (because we don't count the first day)
After two weeks (14 days):
1 penny ×
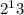 = 8,192 pennies, or $81.92
= 8,192 pennies, or $81.92
After three weeks (21 days) for Purse A we get:
$1,000 + (20 days × $200/day) = $1,000 + $4,000 = $5,000
And for Purse B:
1 penny ×
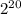 = 1,048,576 pennies, or $10,485.76
= 1,048,576 pennies, or $10,485.76
Now, let's see which purse contains more money after 30 days:
Purse A: $1,000 + (29 days × $200/day) = $1,000 + $5,800 = $6,800
Purse B:

After 30 days, Purse B contains significantly more money due to the power of compound interest.