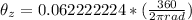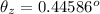Question

You use 8x binoculars were used on a warbler (14cm long) in a tree 18cm away. What angle (in degrees) does the image of the warbler subtend on your retina?

Answer 1

The angle it subtend on the retina is
`\theta_z = 0.44586^o`

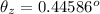
Step-by-step explanation:

From the question we are told that

The length of the warbler is
`L = 14cm = (14)/(100) = 0.14m`

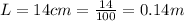
The distance from the binoculars is
`d = 18cm = (18)/(100) = 0.18m`

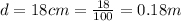
The magnification of the binoculars is
`M =8`

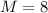
Without the 8 X binoculars the angle made with the angular size of the object is mathematically represented as

`\theta = (L)/(d)`

`\theta = (0.14)/(0.18)`

`= 0.007778 rad`

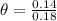
Now magnification can be represented mathematically as

`M = (\theta _z)/(\theta)`

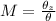
Where
`\theta_z` is the angle the image of the warbler subtend on your retina when the binoculars i.e the binoculars zoom.

So

`\theta_z = M * \theta`

=>
`\theta_z =8 * 0.007778`

`= 0.0622222224`

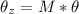
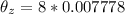
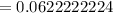
Generally the conversion to degrees can be mathematically evaluated as

`\theta_z = 0.062222224 * ((360 )/(2 \pi rad) )`

`\theta_z = 0.44586^o`