Answer:
The likelihood that a point chosen inside the square will also be inside the circle: 78.54%
Explanation:
- Let x is the side of the suqare
=> the area of the square is:

- Let d is the diameter of the circle
=> the area of the circle :
 π
π
However, d=x because of the square property
<=> the area of the circle :
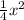 π
π
The likelihood that a point chosen inside the square will also be inside the circle:
the area of the circle / the area of the square
=
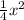 π /
π /

=
 π *100%
π *100%
= 0.7854 * 100%
= 78.54%