Question

A simple random sample of size n=250 individuals who are currently employed is

asked if they work at home at least once per week. Of the 250 employed
individuals surveyed, 26 responded that they did work at home at least once per
week. Construct a 99% confidence interval for the population proportion of
employed individuals who work at home at least once per week.
The lower bound is ____

(Round to three decimal places as needed.)

Answer 1

`0.104 - 2.58\sqrt{(0.104(1-0.104))/(250)}=0.054`

`0.104 + 2.58\sqrt{(0.104(1-0.104))/(250)}=0.154`

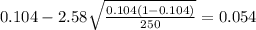
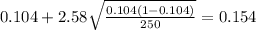
The 99% confidence interval would be given by (0.054;0.154) . So we are confident at 99% that the true proportion of people that they did work at home at least once per week is between 0.054 and 0.154

Explanation:

For this case we can estimate the population proportion of people that they did work at home at least once per week with this formula:

`\hat p = (X)/(n)= (26)/(250)= 0.104`

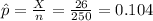
We need to find the critical value using the normal standard distribution the z distribution. Since our condifence interval is at 99%, our significance level would be given by
`\alpha=1-0.99=0.01` and
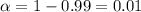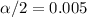`\alpha/2 =0.005`. And the critical value would be given by:

`z_(\alpha/2)=-2.58, z_(1-\alpha/2)=2.58`

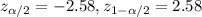
The confidence interval for the mean is given by the following formula:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}`

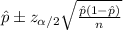
If we replace the values obtained we got:

`0.104 - 2.58\sqrt{(0.104(1-0.104))/(250)}=0.054`

`0.104 + 2.58\sqrt{(0.104(1-0.104))/(250)}=0.154`

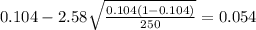
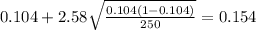
The 99% confidence interval would be given by (0.054;0.154) . So we are confident at 99% that the true proportion of people that they did work at home at least once per week is between 0.054 and 0.154