Answer:
(1, 14)
Explanation:
Given functions:
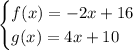
Substitute the function notation for y to create a system of equations:
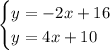
To find the points of intersection of the given functions, solve the system of equations.
Multiply the first equation (function f(x)) by 2:
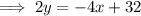
Add this to the second equation (function g(x)) to eliminate x:
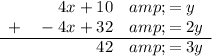
Solve for y:
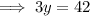
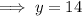
Substitute the found value of y into one of the equations and solve for x:
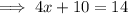
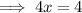
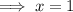
Therefore, the point of intersection of the given functions is (1, 14).