Question

Line segment BA is tangent to the circle.

A circle is shown. Secant D B and tangent B A intersect at point B outside of the circle. Secant D B intersects the circle at point C. The length of A B is x, the length of B C is 55, and the length of C D is 120.


What is the length of line segment BA? Round to the nearest unit.

Answer 1

D. 98 units

Explanation:

Answer 2

Hence the length of line segment BA as 98 units

Explanation:

Given:

BA as tangent to circle ,DB as secant which intersect at point C at circle

Length BC= 55 and CD=120

To Find:

Length of line segment AB.

Solution:

This follows the relationship between tangent and secant in circle terms as:

Consider as figure such that ,

AB as tangent , DB as secant C be point at circle

So secant total distance = DB=BC+CD =55+120=175

Using formula as ,

`AB^2=BC(BC+CD)`

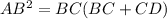
We have to find AB

Here BC=55 and CD=120

`AB^2=55(120+55)`

`AB^2=55(175)`

`AB^2=9625`

`AB=98.10`

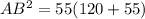
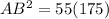
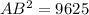
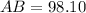
So nearest unit for length will be 98

Hence the length of line segment BA as 98 units