Question

The diameter of a circleis 170inches. The circle has two chords of length 26 inches. What is the distance from each chord to the center of the circle?

Answer 1

Hence the Distance from each other chord to center is 84 inches.

Explanation:

Given:

Diameter =170 inches

2 chords with each length =26 inches.

To Find:

Distance of each chord from the circle.

Solution:

Consider a circle with center as O ,

And OA as Radius

(Refer the attachment)

So as chord be BC and DE respectively with each of 26 length

They have both same length so they should located at same distance from center but as mirror images of each other opposite side of the diameter as shown in fig.

Hence we can calculate for one chord as follows:

Radius =diameter/2=170/2=85

r=85 inches.

Let distance from center t o chord be 'x'

Now draw perpendicular to chord BC with F as midpoint for chord and join endpoints of chord to the center which forms triangle OFC as right angled triangle,

By using pythagorus Theorem

`OC^2=FC^2+OF^2`

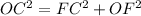
Here OC=85 inches , FC=26/2=13 inches.

So

`85^2=13^2+OF^2`

`OF^2=85^2 -13^2`

`OF^2=7225-169`

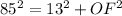
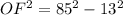
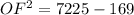
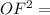`OF^2=`7056

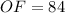`OF=84` inches

Hence the Distance from each other chord to center is 84 inches.