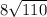Question

What is the area of a triangle whose sides measure 12 inches, 14 inches, and 18 inches?

Enter your answer, in simplified radical form, in the box.

Answer 1

8*sqrt(110)

Explanation:

Answer 2

A =
`8√(110)`
`inches^(2)`

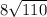
Explanation:

In this question, we are tasked with calculating the area of a triangle given the length of its three sides

Mathematically, we can calculate this using the Heron's formula

For Heron's formula, A =
`√(S(S-A)(S-B)(S-C))`

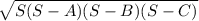
WHERE S =
`(A+B+C)/(2)`

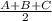
we take the lengths of the triangle as A,B and C respectively as given

S = (12 + 14 + 18)/2 = 22

Plugging the values into the equation, we have;

A =
`√(22(22-12)(22-14)(22-18))\\ \\√(22(10)(8)(4)) \\\\√(7040)`

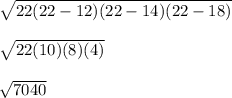
A =
`8√(110)`
`inches^(2)`