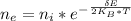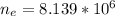Answer:
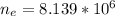
Step-by-step explanation:
Given that;
The energy gap between the valence band and the conduction band in the widely-used semiconductor gallium arsenide (GaAs) is Δ = 1.424 eV.
So; that implies that:
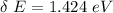
Suppose that we consider a small piece of GaAs with 1020 available electrons, -- This is taking about the numbers of electrons used which is :
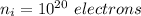
Temperature is given as:
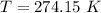
Number of electrons can be calculated by using the formula;