Question

A pilot study evaluated daily dietary intake of a wide range of nutrients among professional female athletes. The main nutrients of interest were total fat (grams) and calcium (mg). The athletes were grouped by age, such that the two groups of interest were 18-29 year olds vs. 30-39 year olds. Your assignment is to perform descriptive analysis of the data, in addition to using both parametric and non-parametric tests to evaluate the same age group differences. By comparing the two classes of test you will see how different their results can be in the same data set. You should: (1) examine the raw distributions of the nutrients for evidence of normality (compare mean and median, look at graphs); (2) perform T-tests for age group differences in fat and calcium; (3) perform the Wilcoxon rank sum test for age group differences in calcium; (4) perform the test for the linear relationship of fat and calcium using Spearman correlation; and (5) answer the questions on the worksheet.

Answer 1

Check the explanation

Explanation:

(1) Consider Age Group 1 (i.e. 18-29 years)

Variable Mean Median

fat 23.94 18.10

Kindly check the first attached image below to see the graph.

Descriptive Statistics: Age Group 2 (i.e. 30-39 years)

Variable Mean Median

Fat 31.98 25.00

Kindly check the second attached image below to see the graph.

Descriptive Statistics: Age Group 1

Variable Mean Median

Calcium 44.41 43.20

Kindly check the third attached image below to see the graph.

Descriptive Statistics: Age Group 2

Variable Mean Median

Calcium 29.27 22.30

Kindly check the fourth attached image below to see the graph.

From the four plots below we can assume that the observations under each groups for Calcium and for that of fat separately follow normal distribution.

(2) Now we want to test whether there is any difference between fat and calcium under each age group pair T-test :

For Age group 1:

Paired T-Test and CI: Fat1, Calcium 1

Paired T for Fat1 - Calcium 1

N Mean StDev SE Mean

Fat1 20 18.27 8.98 2.01

Calcium 1 20 44.41 22.83 5.11

Difference 20 -26.14 14.71 3.29

95% CI for mean difference: (-33.02, -19.25)

T-Test of mean difference = 0 (vs not = 0): T-Value = -7.95 P-Value = 0.000<0.05

Hence there is significance difference between fat and calcium under Age Group 1.

Paired T-Test and CI: Fat2, Calcicum 2

Paired T for Fat2 - Calcicum 2

N Mean StDev SE Mean

Fat2 21 31.98 17.32 3.78

Calcicum 2 21 29.27 22.57 4.92

Difference 21 2.71 5.71 1.25

95% CI for mean difference: (0.12, 5.31)

T-Test of mean difference = 0 (vs not = 0): T-Value = 2.18 P-Value = 0.041<0.05.

Hence there is significance difference between fat and calcium under Age Group 2.

(3)

Wilcoxon rank sum test for age group differences in calcium:

We order the 20+21=41 observations from least to greatest and rank them 1 to 41.

4.0(y), 6.0(y), 6.0(y), 8.0(y), 10.0(y), 10.4(x), 10.6(y), 11.0(y), 14.0(y), 15.0(x), 15.8(x), 16.0(y), 19.0(y),

Rank 1 2 3 4 5 6 7 8 9 10 11 12 13

20.0(x), 22.0(x), 22.3(y), 25.0(x), 26.0(y), 30.0(x), 30.7(y), 32.0(x), 35.0(y), 38.0(x), 40.0(y), 40.9(x)

Rank 14 15 16 17 18 19 20 21 22 23 24 25

45.0(y),45.5(x), 50.0(y), 50.2(x) 55.0(y), 55.1(x), 57.0(x), 60.0(x), 60.1(y), 65.0(y), 65.5(x), 70.0(x), 75.0(x),

Rank 26 27 28 29 30 31 32 33 34 35 36 37 38

80.0(x), 80.8(x), 80.9(y)

Rank 39 40 41

W=sum of ranks assigned to the y's=1+2+3+4+5+7+8+9+12+13+16+18+20+22+24+26+28+30+34+35+41=358

Since sample size is large, so we use following test statistic for testing the differences in calcicum between two groups.

`W^*=\frac{W-(21* 42)/(2)}{\sqrt{(20*21* 42)/(12)}}=-2.1648\\ We~reject~the ~null~hypothesis~that~there~is~no~difference~between~\\ calcium~for~two~age~groups~if~|W^*|>\tau_(0.025)=1.96\\ Hence ~there~is~difference~between~calcium~of~two~age~groups.`

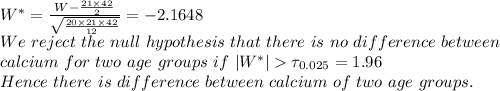
(4)

For age group 1:

Spearman correlation of Fat1 and Calcium 1 = 0.940

P-Value = 0.000<0.05

Hence there is significant linear relationship between fat and calcium under age group 1.

Spearman correlation of Fat2 and Calcicum 2 = 0.994

P-Value = 0.000<0.05

Hence there is significant linear relationship between fat and calcium under age group 2.