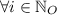Answer:
a)
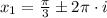 ,
,
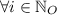 ,
,
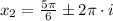 ,
,
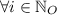 , b)
, b)
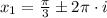 ,
,
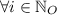 ,
,
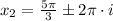 ,
,
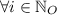
Explanation:
a) The equation must be rearranged into a form with one fundamental trigonometric function first:
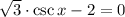

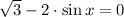
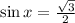

Value of x is contained in the following sets of solutions:
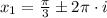 ,
,
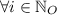
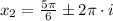 ,
,
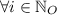
b) The equation must be simplified first:
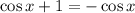

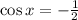

Value of x is contained in the following sets of solutions:
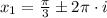 ,
,
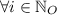
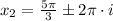 ,
,