Question

1. (Sec. 6.1) In a random sample of 80 components of a certain type, 12 are found to be defective. (a) Give a point estimate for the proportion of all such components that are not defective. (b) A system is to be constructed by randomly selecting two of these components and connecting them in a series. The series will function only if neither component is defective. Give an estimate for the proportion of all such systems that will function properly.

Answer 1

(a) 0.85

(b) 0.7225

Explanation:

(a) The point estimate for the proportion of all such components that are not defective is given by the number of non-defective units in the sample divided by the sample size:

`p=(80-12)/(80)\\p=0.85`

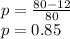
The proportion is 0.85.

(b) Assuming that the sample is large enough to accurately provide a point estimate for the whole population, this can be treated as a binomial model with probability of success (non-defective part) p = 0.85. Since both components must be non-defective for the system to work, the probability of two successes in two trials is:

`P(x=2) = 0.85^2\\P(x=2) = 0.7225`

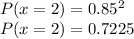
An estimate of 0.7225 for the proportion of all such systems that will function properly.