Answer:
Explanation:
Hello!
The researcher's objective is to test if the variance of the annual repair costs increases with the age of the automobile, i.e. the older the car, the more the repairs costs. The parameters of the study are the population variances of the annual repair costs of 4 years old cars and 2 years old cars.
X₁: Costs of annual repair of a 4 years old car.
Assuming X₁~N(μ₁;δ₁²)
A sample of 26 automobiles 4 years old showed a sample standard deviation for annual repair costs of $170
n₁= 26 and S₁= $170
X₂: Costs of annual repair of a 2 years old car.
Assuming X₂~N(μ₂;σ₂²)
A sample of 25 automobiles 2 years old showed a sample standard deviation for the annual repair cost of $100.
n₂= 25 and S₂= $100
a. State the null and alternative versions of the research hypothesis that the variance in annual repair costs is larger for older automobiles.
H₀: δ₁² ≤ σ₂²
H₁: δ₁² > σ₂²
b. At a .01 level of significance, what is your conclusion? What is the p-value? Discuss the reasonableness of your findings.
This is a variance ratio test and you have to use a Snedecor's F-statistic:
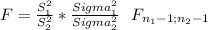

This test is one-tailed to the right and so is the p-value, you have to calculate it under a F₂₅;₂₄
P(F₂₅;₂₄≥2.89)= 1 - P(F₂₅;₂₄<2.89)= 1 - 0.994= 0.006
Using the p-value approach the decision rule is:
If p-value ≤ α, reject the null hypothesis.
If p-value > α, do not reject the null hypothesis.
α: 0.01
The p-value is less than the level of significance, the decision is to reject the null hypothesis.
Then using a 1% level, you can conclude that the population variance of the cost of annual repairs for 4 years old cars is greater than the population variance of the cost of annual repairs for 2 years old cars.
I hope this helps!