Question

1. Prove that quadrilateral DOGS is

a parallelogram. The coordinates

of DOGS are D(1, 1), (2, 4),

G(5, 6), and S(4,3).

-108

-6

-4

4

6

8

10

S doo

Page

1

1

2

-

+

Answer 1

DOGS is a parallelogram.

Explanation:

Given the quadrilateral DOGS with coordinates D(1, 1), O(2, 4), G(5, 6), and S(4,3).

To prove that it is a parallelogram, we need to show that the opposite lengths are equal. That is:

• |DO|=|GS|
• |OG|=|SD|

Using the Distance Formula

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

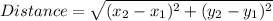
For D(1, 1) and O(2, 4)

`|DO|=√((2-1)^2+(4-1)^2)=√(1^2+3^2)=√(10) \:Units`

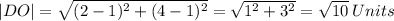
For G(5, 6), and S(4,3).

`|GS|=√((4-5)^2+(3-6)^2)=√((-1)^2+(-3)^2)=√(10)\:Units`

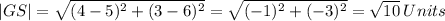
For O(2, 4) and G(5, 6)

`|OG|=√((5-2)^2+(6-4)^2)=√((3)^2+(2)^2)=√(13)\:Units`

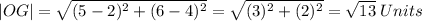
For S(4,3) and D(1, 1)

`|SD|=√((1-4)^2+(1-3)^2)=√((-3)^2+(-2)^2)=√(13)\:Units`

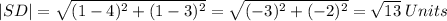
Since:

• |DO|=|GS|
• |OG|=|SD|

Then, quadrilateral DOGS is a parallelogram.