Question

A data set includes 103 body temperatures of healthy adult humans having a mean of 98.9degreesf and a standard deviation of 0.67degreesf. construct a 99​% confidence interval estimate of the mean body temperature of all healthy humans. what does the sample suggest about the use of 98.6 degreesf as the mean body​ temperature?

Answer 1

The true mean body temperature of healthy humans may not be exactly 98.6°F.

To construct a confidence interval for the mean body temperature of all healthy humans, you can use the following formula:

Confidence Interval= X ±Z(
`(S)/(√(n) )`)

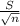where:

X is the sample mean,

Z is the Z-score corresponding to the desired confidence level,

S is the sample standard deviation,

n is the sample size.

Given that the sample mean

X =98.9, the sample standard deviation

S=0.67, and the sample size

n=103, and you want a 99% confidence interval, you need to find the Z-score corresponding to the middle 99% of the standard normal distribution.

For a 99% confidence interval, you can find the Z-score using a Z-table or a statistical software. For a two-tailed interval (which is common), the Z-score would be approximately 2.576.

Now, plug in the values into the formula:

Confidence Interval=98.9±2.576(
`(0.67)/(√(103) )`)

​Calculate the margin of error:

Margin of Error=2.576×
`(0.67)/(√(103) )`

Finally, construct the confidence interval:

Confidence Interval=(98.9−Margin of Error,98.9+Margin of Error)

This will give you the range within which you can be 99% confident that the true mean body temperature of all healthy humans lies.

As for the use of 98.6°F as the mean body temperature, if this value falls within the confidence interval you calculated, it suggests that the true mean body temperature of healthy humans may not be exactly 98.6°F. The interval provides a range of values that are statistically plausible for the true mean.

Answer 2

Explanation:

Confidence interval is written in the form,

(Sample mean - margin of error, sample mean + margin of error)

The sample mean, x is the point estimate for the population mean.

Margin of error = z × s/√n

Where

s = sample standard deviation = 0.67

n = number of samples = 103

From the information given, the population standard deviation is unknown hence, we would use the t distribution to find the z score

In order to use the t distribution, we would determine the degree of freedom, df for the sample.

df = n - 1 = 103 - 1 = 102

Since confidence level = 99% = 0.99, α = 1 - CL = 1 – 0.99 = 0.01

α/2 = 0.01/2 = 0.005

the area to the right of z0.005 is 0.005 and the area to the left of z0.005 is 1 - 0.005 = 0.995

Looking at the t distribution table,

z = 2.6249

Margin of error = 2.6249 × 0.67/√103

= 0.173

Confidence interval = 98.6 ± 0.173

This suggests that the mean body temperature could very possibly be

98.6degrees°F.