Question

Suppose that the population of the scores of all high school seniors that took the SAT-M (SAT math) test this year follows a Normal distribution, with mean μ and standard deviation σ = 100. You read a report that says, "On the basis of a simple random sample of 100 high school seniors that took the SAT-M test this year, a confidence interval for μ is 512.00 ± 25.76." The confidence level for this interval is

Answer 1

The confidence level for this interval is 99%.

Explanation:

The margin of error M has the following equation.

`M = z*(\sigma)/(√(n))`

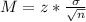
In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

z is related to the confidence level.

In this problem:

`M = 25.76, \sigma = 100, n = 100`

So

`25.76 = z*(100)/(√(100))`

`10z = 25.76`

`z = 2.576`

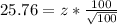
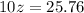
Looking at the z table,
`z = 2.576` has a pvalue of 0.995.

So the confidence level is:

`1 - 2(1 - 0.995) = 1 - 0.01 = 0.99`

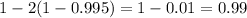
The confidence level for this interval is 99%.