Your Question is not well presented.
See Question Below
Which table has a constant of proportionality between y and x of 1/6? (choose 1 answer.)
A:
x--> 15 ---19
 --- 36
--- 36
y--> 5 ---- 6
 ---- 12
---- 12
B:
x--> 12 ---13
 --- 24
--- 24
y--> 2 ---- 3
 ---- 14
---- 14
C:
x--> 18 --- 27 --- 33
y--> 3 ---- 4
 ---- 5
---- 5

Answer:
Table C has 1/6 as the constant of proportionality between y and x
Explanation:
Given
Table A, B, C
Required
To check which of the tables has a constant of proportionality of 1/6
The constant of proportionality is calculated by dividing individual values of y column with x column.
Mathematically, this is represented by

Where k is the constant of proportionality
Recall Table A
x--> 15 ---19
 --- 36
--- 36
y--> 5 ---- 6
 ---- 12
---- 12
When x = 15, y = 5.
The constant of proportionality becomes

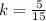 --- Simplify fraction to lowest term by dividing by 5
--- Simplify fraction to lowest term by dividing by 5
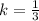
So, when x = 15, y = 5.
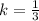
 is not equal to
is not equal to
 ; So, we do not need to check further in table A.
; So, we do not need to check further in table A.
Hence, table A does not have 1/6 as the constant of proportionality between y and x
We move to table B
Recall Table B
x--> 12 ---13
 --- 24
--- 24
y--> 2 ---- 3
 ---- 14
---- 14
When x = 12, y = 2.
The constant of proportionality becomes

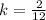 --- Simplify fraction to lowest term by dividing by 2
--- Simplify fraction to lowest term by dividing by 2
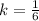
We can't conclude yet, if the constant of proportionality between y and x in table B is
 until we check further
until we check further
When

The constant of proportionality becomes

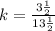 --- Convert to decimal
--- Convert to decimal
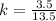 Simplify fraction to lowest term by dividing by 0.5
Simplify fraction to lowest term by dividing by 0.5
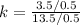
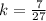 -- This cannot be simplified any further
-- This cannot be simplified any further
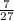 is not equal to
is not equal to
 ; So, we do not need to check further in table B.
; So, we do not need to check further in table B.
Hence, table B does not have 1/6 as the constant of proportionality between y and x
We move to table C
Recall Table C
x--> 18 --- 27 --- 33
y--> 3 ---- 4
 ---- 5
---- 5

When x = 18, y = 3
The constant of proportionality becomes

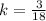 --- Simplify fraction to lowest term by dividing by 3
--- Simplify fraction to lowest term by dividing by 3
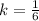
We can't conclude yet, if the constant of proportionality between y and x in table C is
 until we check further
until we check further
When x = 27,
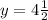
The constant of proportionality becomes

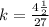 --- Convert to fraction to decimal
--- Convert to fraction to decimal
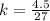 Simplify fraction to lowest term by dividing by 4.5
Simplify fraction to lowest term by dividing by 4.5
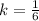
We still can't conclude until we check further
When x = 33,
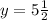
The constant of proportionality becomes

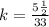 --- Convert to fraction to decimal
--- Convert to fraction to decimal
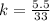 Simplify fraction to lowest term by dividing by 5.5
Simplify fraction to lowest term by dividing by 5.5
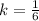
Notice that; for every value of x and its corresponding value of y, the constant of proportionality, k maintains
 as its value
as its value
Hence, we can conclude that "Table C has 1/6 as the constant of proportionality between y and x"