Answer:
(a) The mean is 7.5.
The variance is 1.875.
The standard deviation is 1.369.
(b) The event is not unusual.
Explanation:
The random variable X can be defined as the number of U.S. mothers with school-aged children who choose fast food as a dining option for their families one to three times a week.
The proportion of the random variable X is, p = 0.75.
A random sample of n = 10 U.S. mothers with school-aged children are selected and were asked if they choose fast food as a dining option for their families one to three times a week.
The event of a US mother choosing fast food as a dining option for their families one to three times a week is independent of the other mothers.
The random variable X thus follows a Binomial distribution with parameter n = 10 and p = 0.75.
(a)
Compute the mean of the Binomial distribution as follows:
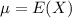

The mean is 7.5.
Compute the variance of the Binomial distribution as follows:

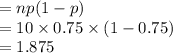
The variance is 1.875.
Compute the standard deviation of the Binomial distribution as follows:


The standard deviation is 1.369.
(b)
The probability mass function of a Binomial distribution is:
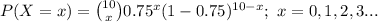
Compute the value of P (X = 10) as follows:
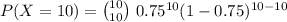
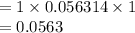
The probability of ten mothers choosing fast food as a dining option for their families one to three times a week is 0.0563.
Unusual events are those events that have a very low probability of happening. The probability of unusual event is generally less than 0.05.
In this case the value of P (X = 10) is 0.0563, approximately 0.06.
So, P (X = 10) ≈ 0.06 > 0.05.
Thus, the event is not unusual.