Question

50 pts!

Determine the points of
intersection:
y = x^2-7
y = 8+2x

1. (_,_)

2. (_,_)

Answer 1

(-3,2) & (5,18)

Explanation:

y = x² - 7

y = 8 + 2x

x² - 7 = 8 + 2x

x² - 2x - 15 = 0

x² - 5x + 3x - 15 = 0

x(x - 5) + 3(x - 5) = 0

(x + 3)(x - 5) = 0

x = -3, 5

y = 8 + 2(-3) = 2

(-3,2)

y = 8 + 2(5) = 18

(5,18)

Answer 2

(5, 18) and (-3, 2)

Explanation:

We have two equations:

`y=x^2-7`

`y=8+2x`

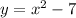
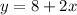
Let's eliminate y by setting the two equations equal:

`x^2-7=8+2x`

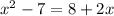
Move all the terms to one side:

`x^2-2x-15=0`

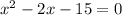
Factor:

`(x-5)(x+3)=0`

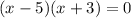
Solve for x:

x - 5 = 0

x = 5

OR

x + 3 = 0

x = -3

Plug each of these values of x into any of the two original equations:

y = 8 + 2 * 5 = 8 + 10 = 18

y = 8 + 2 * (-3) = 8 - 6 = 2

The solutions are (5, 18) and (-3, 2).

Hope this helps!