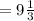Answer:
Length of the longest trail
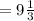
Explanation:
The length of the longest trail will be equal to product of the two trails.
Given -
Length of one trail
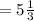
Length of the second trail
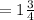
Re writing the fractions, we get -
Length of one trail
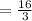
Length of second trail

The length of the longest trail
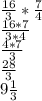
Length of the longest trail