Question

Construct and interpret a 95​% confidence interval for the population proportion of adults in the country who believe that televisions are a luxury they could do without. Select the correct choice below and fill in any answer boxes within your choice.

Answer 1

The 95% confidence interval for the population proportion of adults in the country who believe that televisions are a luxury they could do without is (0.500, 0.562).

Explanation:

The complete question is:

A random sample of 1014 adults in a certain large country was asked "Do you pretty much think televisions are a necessity or a luxury you could do without?" Of the 1014 adults surveyed, 538 indicated that televisions are a luxury they could do without.Construct and interpret a 95% confidence interval for the population proportion of adults in the country who believe that televisions are a luxury they could do without.

Solution:

In a sample of 1014 adults, 538 indicated that televisions are a luxury they could do without.

Compute the sample proportion of adults who indicated that televisions are a luxury they could do without as follows:

`\hat p=(538)/(1014)=0.531`

The (1 - α)% confidence interval for population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

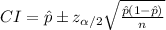
The critical value of z for 95% confidence interval is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

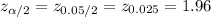
*use a z-table.

Compute the 95% confidence interval for the population proportion of adults in the country who believe that televisions are a luxury they could do without as follows:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

`=0.531\pm 1.96* \sqrt{(0.531(1-0.531)/(1014)}}\\=0.531\pm 0.0307\\=(0.5003, 0.5617)\\\approx (0.500, 0.562)`

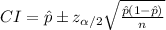
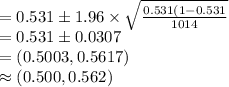
Thus, the 95% confidence interval for the population proportion of adults in the country who believe that televisions are a luxury they could do without is (0.500, 0.562).