Question

. A lightbulb with a resistance of 2.9 ohms is operated using a 1.5-volt battery. At what rate is

electrical energy transformed in the lightbulb?

Answer 1

The rate of electrical energy transformed in the light bulb is 0.78 Joules per seconds.

Step-by-step explanation:

Electrical energy is given by,

E = IVt

The rate of electrical energy transformed in the light bulb can be determined by;

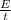`(E)/(t)` = IV

From Ohms law which states that the amount of current passing through a metallic conductor, e.g wire, is directly proportional to the potential difference across its ends, provided that the temperature is constant.

i.e V = IR

where: V is the potential difference, I is the current and R is the resistance of the conductor

So that: R = 2.9 Ohms and V = 1.5 Volt, find I.

⇒ I =
`(V)/(R)`

=
`(1.5)/(2.9)`

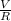
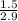
= 0.5172

I = 0.52 A

Then;

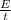`(E)/(t)` = IV

= 0.52 × 1.5

= 0.78 J/s

The rate of electrical energy transformed in the light bulb is 0.78 Joules per seconds.

Answer 2

Step-by-step explanation:

Given that,

A light bulb has a resistance of 2.9ohms

R = 2.9 ohms

And a battery of 1.5V is applied

V = 1.5 V

We want to find the rate of energy transformed

First we need to know what rate of energy is

Rate of energy implies that we want to find power. Power is the rate at which work is done

P = Workdone / time

Then,

In electronic, the power dissipated by a resistor is given as

P = V² / R

P = 1.5² / 2.9

P = 0.7759 W

P ≈ 0.776 W

So, the rate at which electrical energy transformed in the lightbulb is 0.776 Watts