Question

7. (Sec. 7.2) In a survey of 2004 American adults, 501 of them said that they believed in astrology. (a) Calculate and interpret a confidence interval at the 95% confidence level for the proportion of all adult American adults who believe in astrology. (b) Calculate and interpret a 95% lower confidence bound for the proportion of all adult American adults who believe in astrology.

Answer 1

The 95% confidence interval for the proportion for the American adults who believed in astrology is (0.23, 0.27).

This means that we can claim with 95% confidence that the true proportion of all American adults who believed in astrology is within 0.23 and 0.27.

Explanation:

We have to construct a 95% confidence interval for the proportion.

The sample proportion is p=0.25.

`p=X/n=501/2004=0.25`

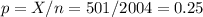
The standard deviation can be calculated as:

`\sigma_p=\sqrt{(p(1-p))/(n)}=\sqrt{(0.25*0.75)/(2004)}=√( 0.000094 )=0.01`

For a 95% confidence interval, the critical value of z is z=1.96.

The margin of error can be calculated as:

`E=z\cdot \sigma_p=1.96*0.01=0.0196`

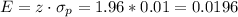
Then, the lower and upper bounds of the confidence interval can be calculated as:

`LL=p-E=0.25-0.0196=0.2304\approx0.23\\\\UL=p+E=0.25+0.0196=0.2696\approx 0.27`

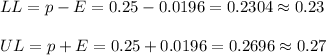
The 95% confidence interval for the proportion for the American adults who believed in astrology is (0.23, 0.27).

This means that we can claim with 95% confidence that the true proportion of all American adults who believed in astrology is within 0.23 and 0.27.

Answer 2

Find the given attachments for complete answer