Question

7500 dollars is placed in an account with an annual interest rate of 7.75%. To the nearest year, how long will it take for the account value to reach 38200 dollars?

Answer 1

It will take approximately 53 years for the account value to reach 38200 dollars

Explanation:

Given the following parameters:

Principal P = 7500

Interest Rate R = 7.75% = 0.0775

Let us find the simple interest for the first year

Simple Interest, I = PRT

with T = 1 year = 12 months

I = 7500 × 0.0775 × 1

= 581.25

The amount for the first year is the addition of the principal and simple interest.

Amount, A = 7500 + 581.25 = 8081.25.

Now, we want to find the time T when Amount A = 38200

Given A = P + I

And I = PRT

A = P + PRT

= P(1 + RT)

Let us make T the subject of the formula.

Dividing both sides by P

A/P = 1 + RT

A/P - 1 = RT

T = ((A/P) - 1)/R

T = ((38200/7500) - 1)/0.0775

= (307/75)/0.0775

= 52.8172043

≈ 53 years.

Answer 2

It will take 55 years for the account value to reach 38200 dollars

Explanation:

This is a simple interest problem.

The simple interest formula is given by:

`E = P*I*t`

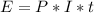
In which E are the earnings, P is the principal(the initial amount of money), I is the interest rate(yearly, as a decimal) and t is the time.

After t years, the total amount of money is:

`T = E + P`.

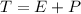In this problem, we ahve that:

`T = 38200, P = 7500, I = 0.075`

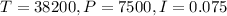
So

First we find how much we have to earn in interest.

`38200 = E + 7500`.

`E = 38200 - 7500`

`E = 30700`

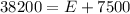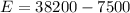
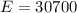
How much time to earn this interest?

`E = P*I*t`

`30700 = 7500*0.075*t`

`t = (30700)/(7500*0.075)`

`t = 54.6`

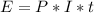
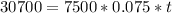
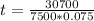
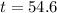
Rounding up

It will take 55 years for the account value to reach 38200 dollars