Question

9. Traditional medical treatment will cure about 88% of all people who suffer from a certain eye

disorder. Suppose a large medical clinic treats 93 people with this disorder using a new state-of-the-

art technique.

a.

Estimate the probability that fewer than 80 patients will recover.

b.

The director of the hospital recommends that all hospitals adopt this new technique

since more than 85 patients in the sample have recovered after being treated with the

new technique. Confirm/disprove the director's claim. Show all your work and interpret

your results.

Answer 1

a) P (Y less than or equal to 79 ) = 0.226

b) Z = 1.008 less than or equal to Zc = 1.64

So, it means null hypothesis is not rejected.

Explanation:

a) Probability that fewer than 80 patients will recover.

As we have:

p = 88% = 0.88 = population success proportion

n = 93 = Sample size

mean = n x p , mean = 93 x 0.88 , mean = 81.84

So, we need P (Y less than or equal to 79) fewer than 80 patients.

Standard Deviation of the population =

SD of population =
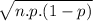`√(n . p . (1-p))` , SD of population =
`√(93 .0.88 .(1-0.88))`

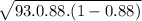
SD of population = 3.13

As we know that,

probability in binomial distribution is approximately equal to normal distribution so, we will use normal distribution from here. In addition, due to this shift 79 will be equal to 79.5 in normal distribution.

P(Y less than or equal to 79) ≈ P(Y less than or equal to 79.5)

P(
`(Y - mean )/(SD)`) , P(
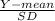`(79.5 - 81.84)/(3.1336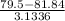)`) , P(Z less than or equal to -0.75)

So, when will you check the Z score of -0.75 in the Z table you will get the probability which is :

P (Y less than or equal to 79 ) = 0.226

So, 0.226 is the probability that fewer than 80 patients will recover.

b) Z test is used in this part to check the claim:

Favorable Cases sample (recovered) = 85 = Y

Sample size = N = 93

Significance level = 0.05

Proportion Sample = p = Y/N = 85/93 = 0.914.

1. Null hypothesis and Alternative Hypothesis:

H1: p less than or equal to 88% or p less than or equal to 0.88

H2: p greater than 88% or p greater than 0.88

2. Rejection Region:

Zc value is = 1.64 for a right tail test.

Rejection region is such that z value must be greater than Zc value i.e 1.64. If it is not greater, it will not lie in rejection region.

3. Statistics Test:

In this we have to calculate value of Z and compare it with value of Zc.

Z =
`(P-p1)/(√(p1(1-p1)/n) )`

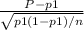
Small p1 = 0.88 , Capital P = 0.914 Z =
`(0.914-0.88)/(√(0.88.(1-0.88)/93) )`

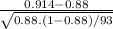
Z = 1.008

4. Final Decision about the null hypothesis:

As we can see, Z value is less than Zc value, hence it does not lie in the rejection region.

Z = 1.008 less than or equal to Zc = 1.64

So, it means null hypothesis is not rejected.

H1 is not rejected, it means there is not sufficient proof to claim that population proportion is larger than population success proportion p1.