Question

A polyethylene rod exactly 10 inches long with a cross-sectional area of 0.04 in2 is used to suspend a weight of 358 lbs-f (pounds-force). Given the tensile modulus for this polymer is 25,000 psi and the viscosity is 1 × 109 psi-sec, calculate the length of the rod, in inches, 1 hour(s) after loading. Answer Format: X.XX Unit: inches

Answer 1

Final length of the rod = 13.90 in

Step-by-step explanation:

Cross Sectional Area of the polythene rod, A = 0.04 in²

Original length of the polythene rod, l = 10 inches

Tensile modulus for the polymer, E = 25,000 psi

Viscosity,
`\eta = 1*10^(9) psi -sec`

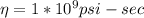
Weight = 358 lbs - f

time, t = 1 hr = 3600 sec

Stress is given by:

`\sigma = (Force)/(Area) \\\sigma = (358)/(0.04) \\\sigma = 8950 psi`

Based on Maxwell's equation, the strain is given by:

`strain = \sigma ( (1)/(E) + (t)/(\eta) )\\Strain = 8950 ( (1)/(25000) + (3600)/(10^(9) ) )\\Strain = 0.39022`

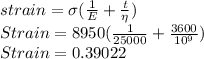
Strain = Extension/(original Length)

0.39022 = Extension/10

Extension = 0.39022 * 10

Extension = 3.9022 in

Extension = Final length - Original length

3.9022 = Final length - 10

Final length = 10 + 3.9022

Final length = 13.9022 in

Final length = 13.90 in