Question

At age 9 the average weight (21.3 kg) and the average height (124.5 cm) for both boys and girls are exactly the same. a random sample of 9-year-olds yielded these results. estimate the mean difference in height between boys and girls with 95% confidence. does your interval support the given claim?

Answer 1

a) Null hypothesis H₀: μ₁ = μ₂

Alternative hypothesis Hₐ: μ₁ ≠ μ₂

b) Critical
`t_(\alpha /2)` is ±1.985523

c) The test statistic t is -0.1276

d) P-value > α = 0.05, we accept the null hypothesis

e) There is sufficient statistical evidence to suggest that the average weight of boys and girls are exactly the same

Explanation:

a) Null hypothesis H₀: μ₁ = μ₂, the average weight of boys and girls are the same

Alternative hypothesis Hₐ: μ₁ ≠ μ₂ the average weight of boys and girls are not the same

b) Sample size, boys, n₁ = 60, girls, n₂ = 50

Mean height, boys,
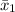`\bar{x}_(1)` = 123.5 cm, girls,
`\bar{x}_(2)` = 126.2 cm

Population variance, boys s₁ = 98, girls, s₂ = 120

The critical value at 95% confidence, degrees of freedom (smaller between n₁ and n₂) df = 50 - 1 = 49, α = (1 - 0.95)/2 = 0.025 the critical t is given from t relations as follows;

Critical
`t_(\alpha /2)` = ±1.985523

c) For the test statistic, we have;

`t=\frac{(\bar{x}_(1)-\bar{x}_(2))-(\mu_(1)-\mu _(2) )}{\sqrt{(s_(1)^(2) )/(n_(1))-(s _(2)^(2))/(n_(2))}}`

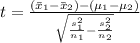
Plugging in the values where μ₁ = μ₂, we have;

The test statistic t = -0.1276

From t relations, we have the p-value , p = 0.8987748

d) Therefore, since the p-value > α = 0.05, we accept the null hypothesis

e) Based on the analysis, there is sufficient statistical evidence to suggest that the average weight of boys and girls are exactly the same.

Answer 2

Complete Question:

Heights of 9-Year-Olds At age 9 the average weight (21.3 kg) and the average height (124.5 cm) for both boys and girls are exactly the same. A random sample of 9-year-olds yielded these results. Estimate the mean difference in height between boys and girls with 95% confidence. Does your interval support the given claim?

Boys Girls

Sample Size 60 50

Mean Height, cm 123.5 126.2

Population variance 98 120

a.State the hypotheses and identify the claim.

b.Find the critical value(s).

c.Compute the test value.

d.Make the decision.

e.Summarize the results.

Explanation:

Find attachments for complete solution