Question

The weights of soy patties sold by a diner are normally distributed. A random sample of 15 patties yields a mean weight of 3.8 ounces with a sample standard deviation of 0.5 ounces. At the 0.05 level of​ significance

Answer 1

Complete Question

The weights of soy patties sold by a diner are normally distributed. A random sample of 15 patties yields a mean weight of 3.8 ounces with a sample standard deviation of 0.5 ounces. At the 0.05 level of significance,perform a hypothesis test to see if the true mean weight is less than 4 ounce.

Answer:

Yes the true mean weight is less than 4 ounce

Step-by-step explanation:

From the question we are told that

The random sample is
`n = 15`

The mean weight is
`\= x = 3.8\ ounce`

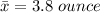
The standard deviation is
`\sigma = 0.5 \ ounce`

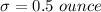
The level of significance is
`\alpha = 0.05`

So

The null hypothesis is
`H_o : \mu \ge 4`

The alternative hypothesis is
`H_a : \mu < 4`

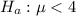
Generally the critical value which a bench mark to ascertain whether the null hypothesis is true or false is mathematically represented as

`t_(0.05) = 1.79`

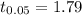
This value is obtained from the critical value table

Generally the test statistics is mathematically represented as

`Test \ Statistics (ST) = (\= x - \mu )/((\sigma)/(√(n) ) )`

=>
`ST = (3.8 -4 )/((0.5)/(√(20) ) )`

`ST = - 1.79`

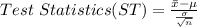
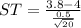
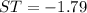
So since ST is less than
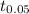`t_(0.05)` then the null hypothesis would be rejected and the alternative hypothesis would be accepted so

Thus the true mean weight is less than 4