Question

Based on the data from six students, the regression equation relating number of hours of preparation (x) and test score (y) is . the same data yield and what is the best predicted test score for a student who spent 10 hours preparing for the test?

Answer 1

78

Explanation:

Answer 2

The predicted test score for a student who spent 10 hours preparing for the test is 78.

Explanation:

The regression equation is used to determine the predicted value of the response or dependent variable based on an explanatory or independent variable.

The general form of a regression equation is:

`y=\alpha +\beta x`

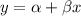
Here,

y = dependent variable

x = independent variable

α = intercept

β = slope

The regression equation relating number of hours of preparation (x) and test score (y) is:

`y=67.3+1.07x`

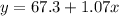
Compute the value of y for x = 10 as follows:

`y=67.3+1.07x`

`=67.3+(1.07* 10)\\=67.3+10.7\\=78`

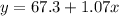
Thus, the predicted test score for a student who spent 10 hours preparing for the test is 78.