Question

Do one of the​ following, as appropriate.​ (a) Find the critical value z Subscript alpha divided by 2​, ​(b) find the critical value t Subscript alpha divided by 2​, ​(c) state that neither the normal nor the t distribution applies. Confidence level 99​%; nequals26​; sigma equals 28.9​; population appears to be normally distributed.

Answer 1

We want to construct a confidence interval at 99% of confidence, so then the significance level would be
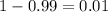`1-0.99 =0.01` and the value of
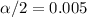`\alpha/2 =0.005`. And for this case since we know the population deviation is not appropiate use the t distribution since we know the population deviation and the best quantile assuming that the population is normally distributed is given by the z distribution.

And if we find the critical value in the normal standard distribution or excel and we got:

`z_(\alpha/2)= \pm 2.576`

And we can use the following excel code:

"=NORM.INV(0.005,0,1)"

Explanation:

For this case we have the following info given:

`\alpha=0.01, n =26, \sigma = 28.9`

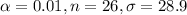
We want to construct a confidence interval at 99% of confidence, so then the significance level would be
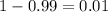`1-0.99 =0.01` and the value of
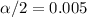`\alpha/2 =0.005`. And for this case since we know the population deviation is not appropiate use the t distribution since we know the population deviation and the best quantile assuming that the population is normally distributed is given by the z distribution.

And if we find the critical value in the normal standard distribution or excel and we got:

`z_(\alpha/2)= \pm 2.576`

And we can use the following excel code:

"=NORM.INV(0.005,0,1)"