Question

A 5-m steel beam is lowered by means of two cables unwinding at the same speed from overhead cranes. As the beam approaches the ground, the crane operators apply brakes to slow the unwinding motion. At the instant considered the deceleration of the cable attached at B is 4 m/s2 , while that of the cable attached at D is 3 m/s2 .

Determine the angular acceleration of the beam.

Answer 1

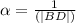`\alpha = (1)/( (\mid BD \mid ))`, (plug in the value of BD to get the answer, you did not provide it in your question)

Step-by-step explanation:

Absolute acceleration of point B,
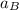`a_(B)` = 4 m/s²

Absolute acceleration for point D,
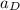`a_(D)` = 3 m/s²

Acceleration of point B relative to D in the normal direction BD,
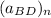`(a_(BD)) _(n)` = 0 (the cable moves with constant velocity)

Acceleration of point B relative to D in the tangential direction to BD,
`(a_(BD))_(t)` = ?

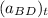The equation for the relative acceleration for the motion between B and D:

`a_(B) = a_(D) + (a_(BD))_(n) + (a_(BD))_(t)\\4 = 3+ 0+ (a_(BD))_(t)\\ (a_(BD))_(t) = 1 m/s^(2)`

To determine the angular acceleration of the beam

`a = \alpha (\mid BD \mid )\\\alpha = (a)/( (\mid BD \mid )) \\\alpha = (1)/( (\mid BD \mid ))`

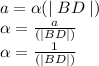
Note: You did not provide the value for the distance between B and D, this value is needed to calculate the angular acceleration. Plug in the value for BD and get your answer