Question

According to industry sources, online banking is expected to take off in the near future. The projected number of households (in millions) using this service is given in the following table. (Here, x = 0 corresponds to the beginning of 1997.)

Year, x 0 1 2 3 4 5
Households, y 4.5 7.5 10.0 13.0 15.6 18.0
(a) Find an equation of the least-squares line for these data. (Give numbers to three decimal places.)
y(x) =

(b) Use your result of part (a) to estimate the number of households using online banking at the beginning of 2007, assuming the projection is accurate.

Answer 1

(a) The least-square regression line is:
`y=4.662+2.709x`.

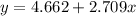(b) The number of households using online banking at the beginning of 2007 is 31.8.

Explanation:

The general form of a least square regression line is:

`y=\alpha +\beta x`

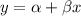
Here,

y = dependent variable

x = independent variable

α = intercept

β = slope

(a)

The formula to compute intercept and slope is:

`\begin{aligned} \alpha &= \frac{\sum{Y} \cdot \sum{X^2} - \sum{X} \cdot \sum{XY} }{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} \\\beta &= \frac{ n \cdot \sum{XY} - \sum{X} \cdot \sum{Y}}{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} \end{aligned}`

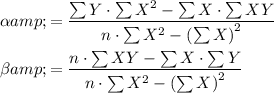
The values of ∑X, ∑Y, ∑XY and ∑X² are computed in the table below.

Compute the value of intercept and slope as follows:

`\begin{aligned} \alpha &= \frac{\sum{Y} \cdot \sum{X^2} - \sum{X} \cdot \sum{XY} }{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} = ( 68.6 \cdot 55 - 15 \cdot 218.9)/( 6 \cdot 55 - 15^2) \approx 4.662 \\ \\\beta &= \frac{ n \cdot \sum{XY} - \sum{X} \cdot \sum{Y}}{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} = ( 6 \cdot 218.9 - 15 \cdot 68.6 )/( 6 \cdot 55 - \left( 15 \right)^2) \approx 2.709\end{aligned}`

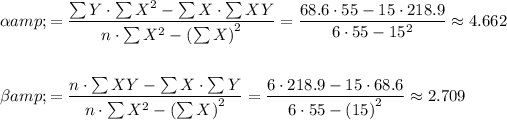
The least-square regression line is:

`y=4.662+2.709x`

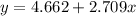
(b)

For the year 2007 the value of x is 10.

Compute the value of y for x = 10 as follows:

`y=4.662+2.709x`

`=4.662+(2.709*10)\\=4.662+27.09\\=31.752\\\approx 31.8`

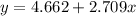
Thus, the number of households using online banking at the beginning of 2007 is 31.8.