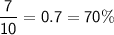Question

each morning, danai buys breakfast on her why to work. In the past thirty days, she bought a bagel on 6 days, a banana on 12 days, a doughnut on 3 days, and an orange on 9 days. If she bought one item per day, what is the probability that she bought either a banana or an orange? Show or explain your work and write you answer in the space provided.

Answer 1

`\sf (7)/(10)=0.7=70\%`

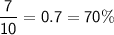
Explanation:

Given information:

• Bagel bought on 6 days
• Banana bought on 12 days
• Doughnut bough on 3 days
• Orange bought on 9 days

Total number of days = 30

Probability Formula

`\sf Probability\:of\:an\:event\:occurring = (Number\:of\:ways\:it\:can\:occur)/(Total\:number\:of\:possible\:outcomes)`

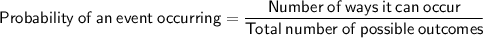
Probability of buying a banana:

`\implies \sf P(Banana)=(12)/(30)`

Probability of buying an orange:

`\implies \sf P(Orange)=(9)/(30)`

Therefore,

`\implies \sf P(Banana) \: or \: P(Orange)=\sf (12)/(30)+(9)/(30)=(21)/(30)=(7)/(10)`

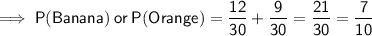
So the probability of buying either a banana or an orange is:

`\sf (7)/(10)=0.7=70\%`

Answer 2

• 0.7 or 70%

Explanation:

Total number of days

• 6 + 12 + 3 + 9 = 30

The number of days she bought a banana or orange

• 12 + 9 = 21

The probability of buying a banana or an orange is

• P(b or o) = 21/30 = 0.7 = 70%