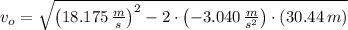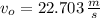Question

A car hits a tree at an estimated speed of 10 mi/hr on a 2% downgrade. If skid marks of 100 ft. are observed on dry pavement (F=0.33) followed by 200 ft. on an unpaved shoulder (F=0.28), what is the initial speed of the vehicle just before the pavement skid was begun?

Answer 1

`v_(o) = 22.703\,(m)/(s)`
`\left(50.795\,(m)/(s)\right)`

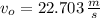
Step-by-step explanation:

The deceleration of the car on the dry pavement is found by the Newton's Law:

`\Sigma F = -\mu_(k,1)\cdot m\cdot g \cdot \cos \theta + m\cdot g \cdot \sin \theta = m\cdot a_(1)`

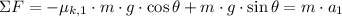
Where:

`a_(1) = (-\mu_(k,1)\cdot \cos \theta + \sin \theta)\cdot g`

`a_(1) = (-0.33\cdot \cos 1.146^(\textdegree)+\sin 1.146^(\textdegree))\cdot \left(9.807\,(m)/(s^(2)) \right)`

`a_(1) = -3.040\,(m)/(s^(2))`

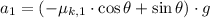
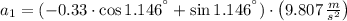
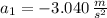
Likewise, the deceleration of the car on the unpaved shoulder is:

`a_(2) = (-\mu_(k,2)\cdot \cos \theta + \sin \theta)\cdot g`

`a_(2) = (-0.28\cdot \cos 1.146^(\textdegree)+\sin 1.146^(\textdegree))\cdot \left(9.807\,(m)/(s^(2)) \right)`

`a_(2) = -2.549\,(m)/(s^(2))`

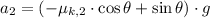
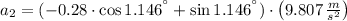
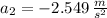
The speed just before the car entered the unpaved shoulder is:

`v_(o) = \sqrt{\left(4.469\,(m)/(s) \right)^(2)-2\cdot \left(-2.549\,(m)/(s^(2)) \right)\cdot (60.88\,m)}`

`v_(o) = 18.175\,(m)/(s)`

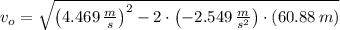
And, the speed just before the pavement skid was begun is:

`v_(o) = \sqrt{\left(18.175\,(m)/(s) \right)^(2)-2\cdot \left(-3.040\,(m)/(s^(2)) \right)\cdot (30.44\,m)}`

`v_(o) = 22.703\,(m)/(s)`
`\left(50.795\,(m)/(s)\right)`