Question

A certain insecticide kills 60% 60 % of all insects in laboratory experiments. A sample of 7 insects is exposed to the insecticide in a particular experiment. What is the probability that exactly 4 insects will survive? Round your answer to four decimal places.

Answer 1

Answer: The probability that exactly 4 insects will survive = 0.2903.

Explanation:

Given : The proportion of all insects in laboratory experiments killed by insecticide = 60%=0.60

Since , by using insecticide only two outcomes are possible either it kills or not kills , so we can use binomial.

Sample size of insects = 7

By using binomial probability formula :
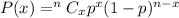`P(x)=^nC_xp^x(1-p)^(n-x)`, where x is binomial variable , n = sample size and p is the probability of getting success.

Let x be the number of insects survived.

As per given , we have

n=7 , p=0.60

Now , the probability that exactly 4 insects will survive :

`P(x=4)= ^7C_4(0.60)^4(1-0.60)^3\\\\=(7!)/(4!3!)(0.60)^4(0.40)^3\\\\= 35* 0.1296* 0.064 \\\\=0.290304\approx0.2903`

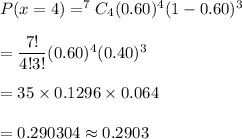
Hence, the probability that exactly 4 insects will survive = 0.2903