Question

A certain forest covers an area of 2600 km2. Suppose that each year this area decreases by 7.75%. What will the area be like after 15 years?

Answer 1

`A(t) = 2600 (1-0.0775)^t = 2600 (0.9225)^t`

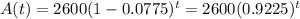
And since the question wants the value for the area at t = 15 years from know we just need to replace t=15 in oir model and we got:

`A(15) = 2600 (0.9225)^(15) = 775.299`

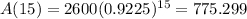
So then we expect about 775.299 km2 remaining for the area of forests.

Explanation:

For this case we can use the following model to describe the situation:

`A = A_o (1 \pm r)^(t)`

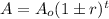
Where
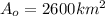`A_o = 2600 km^2` represent the initial area

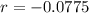`r =-0.0775` represent the decreasing rate on fraction

A represent the amount of area remaining and t the number of years

So then our model would be:

`A(t) = 2600 (1-0.0775)^t = 2600 (0.9225)^t`

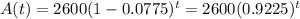
And since the question wants the value for the area at t = 15 years from know we just need to replace t=15 in oir model and we got:

`A(15) = 2600 (0.9225)^(15) = 775.299`

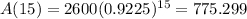
So then we expect about 775.299 km2 remaining for the area of forests.

Answer 2

After 15 years, the area will be of 775.3 km²

Explanation:

The equation for the area of the forest after t years has the following format.

`A(t) = A(0)(1-r)^(t)`

In which A(0) is the initial area and r is the yearly decrease rate.

A certain forest covers an area of 2600 km2.

This means that
`A(0) = 2600`

Suppose that each year this area decreases by 7.75%.

This means that
`r = 0.0775`

So

`A(t) = 2600(1-0.0775)^(t)`

`A(t) = 2600(0.9225)^(t)`

What will the area be like after 15 years?

This is
`A(15)`

`A(t) = 2600(0.9225)^(t)`

`A(15) = 2600(0.9225)^(15) = 775.3`

After 15 years, the area will be of 775.3 km²