Question

A circular saw spins at 6000 rpm , and its electronic brake is supposed to stop it in less than 2 s. As a quality-control specialist, you're testing saws with a device that counts the number of blade revolutions. A particular saw turns 75 revolutions while stopping.Does it meet its specs?

a.yes

b.no

Answer 1

a. yes

Step-by-step explanation:

The initial speed of the circular saw is:

`\dot n_(o) = (6000)/(60) \,(rev)/(s)`

`\dot n_(o) = 100\,(rev)/(s)`

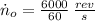
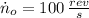
Deceleration rate needed to stop the circular saw is:

`\ddot n = -(100\,(rev)/(s) )/(2\,s)`

`\ddot n = - 50\,(rev)/(s^(2))`

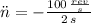
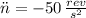
The number of turns associated with such deceleration rate is:

`\Delta n = (\dot n^(2))/(2\cdot \ddot n)`

`\Delta n = (\left(100\,(rev)/(s) \right)^(2))/(2\cdot \left(50\,(rev)/(s^(2)) \right))`

`\Delta n = 100\,rev`

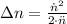
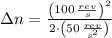
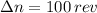
Since the measured number of revolutions is lesser than calculated number of revolution, the circular saw meets specifications.