Question

A certain company makes 12-volt car batteries. After many years of product testing, the company knows that the average life of a battery is normally distributed, with a mean of 50 months and a standard deviation of 9 months. If the company does not want to make refunds for more than 10% of its batteries under the full-refund guarantee policy, for how long should the company guarantee the batteries (to the nearest month)

Answer 1

The company should guarantee the batteries (to the nearest month) for 38 months.

Explanation:

We have here a normally distributed data. The random variable is the average life of the batteries.

From question, we can say that this random variable has a population mean of 50 months and population standard deviation of 9 months. We can express this mathematically as follows:

`\\ \mu = 50` months.

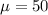`\\ \sigma = 9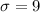` months.

The distribution of the random variable (the average life of the batteries) is the normal distribution, and it is determined by two parameters, namely, the mean
`\\ \mu` and
`\\ \sigma`, as we already know.

For the statement: "The company does not want to make refunds for more than 10% of its batteries under the full-refund guarantee policy", we can say that it means that we have determine, first, how many months last less of 10% of the batteries that its average life follows a normal distribution or are normally distributed?

To find this probability, we can use the standard normal distribution, which has some advantages: one of the most important is that we can obtain the probability of any normally distributed data using standardized values given by a z-score, since this distribution (the normal standard) has a mean that equals 0 and standard distribution of 1.

Well, the z-score is given by the formula:

`\\ z = (x - \mu)/(\sigma)` [1]

Where, x is a raw score coming from a normally distributed data. This is the value that we have to transform into a z-score, that is, in a standardized value.

However, from the question, we want to know what value of z represents a cumulative probability of 10% in the cumulative standard normal distribution. We can find it using the standard normal table, available in Statistics books or on the Internet (of course, we can use also Statistics packages or even spreadsheets to find it).

Then, the value of z is, approximately, -1.28, using a cumulative standard normal table for negative values for z. If the cumulative standard normal only has positive values for z, we can obtain it, using the following:

`\\ P(z<-a) = 1 - P(z<a) =P(z>a)`

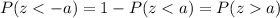
That is, P(z<-1.28) = P(z>1.28). The probability for P(z<1.28) is approximately, 90%.

Therefore, using the formula [1]:

`\\ z = (x - \mu)/(\sigma)`

`\\ -1.28 = (x - 50)/(9)`

`\\ -1.28 * 9 = x - 50`

`\\ -11.52 = x - 50`

`\\ -11.52 + 50 = x`

`\\ 38.48 = x`

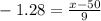
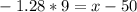
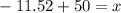
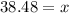
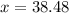`\\ x = 38.48` months.

That is, less than 10% of the batteries have a average life of 38.48 months. Thus, the company should guarantee the batteries (to the nearest month) for 38 months.

Answer 2

A certain company makes 12-volt car batteries. After many years of product testing, the company knows that the average life of a battery is normally distributed, with a mean of 50 months and a standard deviation of 9 months. If the company does not want to make refunds for more than 10% of its batteries under the full-refund guarantee policy, for how long should the company guarantee the batteries?

The company should guarantee the batteries for 38 months.

Explanation:

Using standard normal table,

P(Z < z) = 10%

=(Z < z) = 0.10

= P(Z <- 1.28 ) = 0.10

z = -1.28

Using z-score formula

x = zσ + μ

x = -1.28 *9+50

x = 38

Therefore, the company should guarantee the batteries for 38 months.