Answer:
Answer A.
Explanation:
Recall that
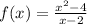
we will calculate the lateral limits of f when x approches x=2. Note that
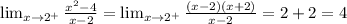
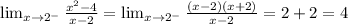
We can clasify the discontinuity as follows:
- Removable discontinuity if both lateral limits are equal and finite.
- Jump discontinuity if both lateral limits are finite but different.
- Essential discontinuity if one of the limits is not finite and the other one is finite.
Based on this classification, since both lateral limits are equal, the discontinuity is a removable discontinuity