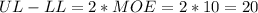Question

A certain small town has a population of 5000 residents. You want to calculate a confidence interval for the average number of gallons of gas bought per month by the residents of this town. You want to be 95% confident that the true value of the population mean is within your interval, and you need to have a margin of error no higher than 10 gallons per month. Based on your previous research in simlar towns, you believe that the population standard deviation is 50 galons per month Give the appropriate statistical symbol or formula for each of the foliowing numbers in this 1, 5000= 2. 50 4 What is the value of a? 5, What is the value of α/2 ? 三6. What is the value of Zan? 1. What wil be the width of your confidence interval from the smaller number to the larger number? (Hint Think about how the MOE is related to the width of the confidence interval)

Answer 1

1. 5000 = N

2. 50 = σ

3. 95% = confidence level (1-α)

4. α = 0.05

5. α/2=0.025=2.5%

6. z_(α/2)=-1.96

1. Width of confidence interval UL-LL=20

Explanation:

We have to calculate a 95% confidence interval for the mean (average number of gallons of gas bought per month by the residents of this town).

The margin of error has to be below 10 gallons/month.

The population standard deviation is considered 50 gallons/month.

1. 5000 = N.

This is the population size N for this study, as this is the total population of the town.

2. 50 = σ

This is the value of the population standard deviation σ, as it is estimated from other studies.

3. 95% = (1-α)

This is the confidence level of the interval, and is equal to 1 less the significance level α.

4. α = 0.05

This is calculated from the confidence level. As the confidence level is 95%, the level of significance is 5%.

`1-\alpha=0.95\\\\\alpha=1-0.95\\\\\alpha=0.05`

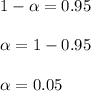
5. α/2=0.05/2=0.025=2.5%

6. The value os z_α/2 is obtained from a standard normal distribution table, where:

`P(z<z_(\alpha/2))=0.025\\\\z_(\alpha/2)=-1.96`

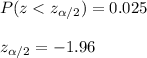
z_α/2=-1.96

1. As the margin of error is 10 (maximum value), the difference between upper and lower bound is:

`UL-LL=2*MOE=2*10=20`