Question

Pls help I’m timed thanks

Answer 1

Picture 1: b

Picture 2: d

Picture 3: c

Explanation:

Hi there,

For Picture 1, to solve for an inverse function, just simply solve for x. Since the closest you can get is arccos(πx)=2y+6, you just

solve for cosine as a function: cos(2y+6)=πx and solving for x:

x= (1/π)cos(2y+6) but since variable choice is arbitrary, you can now redefine y and x:

y= (1/π)cos(2x+6)

For Picture 2, tanx is equivalent to sinx/cosx and cscx is just the reciprocal of sinx. So, it becomes:

`(sinx)/(cosx) *(1)/(sinx) =(1)/(cosx) =cscx`

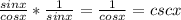
We have already been giving the cosine value of 2, and its inverse is thus 1/2.

For Picture 3, I would recommend revisiting polar coordinates.

Polar coordinates are in the form (r, θ).

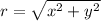`r = \sqrt{x^(2) +y^(2) } }` and θ
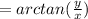`=arctan((y)/(x))` . Recognize there are two possible radii, depending on what side of the circle you start from!

thanks,