Answer:
D . 254.34
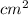
Explanation:
From the diagram,
the diameter of the big circle = 6 cm, and the diameter of the bigger circle = 12 cm.
So,
the diameter of the biggest circle = diameter of the big circle + diameter of the bigger circle
= 6 + 12
= 18 cm
Area of a circle can be determined by;
A =

where:
 is a constant of value
is a constant of value
 ≅ 3.14, 'A' is the area and 'r' is the radius of the circle.
≅ 3.14, 'A' is the area and 'r' is the radius of the circle.
The biggest circles has a radius of
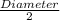
=
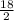
= 9 cm
Thus, the area of the biggest circle =

= 3.14 ×
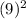
= 3.14 × 81
= 254.34
The area of the biggest circle is 254.34
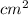 .
.