Answer:
See answer below
Explanation:
Hi there,
To get started, recall the average rate of change formula (essentially the same thing as slope):
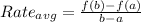
So, just determine the average rate for each function between points [0,2] (a and b for the formula above, respectively).
To make it less time consuming, you do not need to do the division portion as it is same for all of them and (2-0) is greater than 1:

Without even doing the divison of (b-a), we can already see that the function with smallest average rate of change between [0,2] is f(x).
thanks,