Question

A consumer product magazine recently ran a story concerning the increasing prices of CINCO-FONES. The story stated that CINCO-FONE prices dipped a couple of years ago, but now are beginning to increase in price because of added features. According to the story, the average price of all CINCO-FONES a couple of years ago was $215.00. A random sample of n = 22 CINCO-FONES was recently taken and entered into a spreadsheet. It was desired to test to determine if that average price of all CINCO-FONES is now more than $215.00. Find a rejection region appropriate for this test if we are using α = 0.05.

Answer 1

Check the explanation

Explanation:

We have:

Null Hypothesis:

H o:μ = 215

Alternate Hypothesis:

Η α :μ> 215 This is a one tailed test

Standardized value to be tested:

`(new Mean Value - nullValue)/(SE)` ==
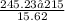`(245.23 – 215)/(15.62)` -= 1.93

Since this is a one tailed test, critical t value which occurs at 95% confidence level is 1.943.

Since 1.93 < 1.943, we can say that At α = 0.05, there is insufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00.

To make it sufficient, we need value more than 1.943.

At α = 0.10, critical t value is 1.440 (less than 1.93) which makes it sufficient.