Question

Show that laplace transform StartSet e Superscript at Baseline t Superscript n EndSetℒeattn​(s)equals=StartFraction n exclamation mark Over (s minus a )Superscript n plus 1 EndFraction n! (s−a)n+1 in two ways. ​

(a) Use the translation property for​ F(s). ​

(b) Use the formula laplace transform StartSet t Superscript n Baseline f (t ) EndSet (s )ℒtnf(t)(s)equals=(negative 1 )Superscript n Baseline StartFraction d Superscript n Over ds Superscript n EndFraction (laplace transform StartSet f EndSet (s ))(−1)n dn dsn(ℒ{f}(s)).

Answer 1

Explanation:

a) The function is:

`f(t)=e^(at)t^n`

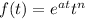
Is is necessary to demonstrate that:

`L[f(t)] = (n!)/((s-a)^(n+1))`

you can use two identities of Laplace's transforms:

`L[t^n]=(n!)/(s^(n+1))\\\\L[e^(at)g(t)]=G(s-a)\\\\`

By using the previous transforms you obtain:

`L[f(t)] = (n!)/((s-a)^(n+1))`

b) The other way is to use the following formula:

`L[t^nf(t)]=(-1)^n(d^n)/(ds^n)F(s)`

Then, you use the following identities:

`L[e^(at)]=(1)/(s-a)\\\\(d^n)/(ds^n)[(1)/(s-a)]=(-1)^n(n!)/((s-a)^(n+1))`

then, by replacing you obtain:

`L[f(t)] = (n!)/((s-a)^(n+1))`