Answer:
The smallest radian solution is 3.14, approximately. And the next smallest radian solution is 1.32, approximately.
Explanation:
The given expression is
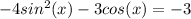
We know that
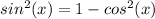
So,
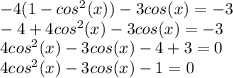
Let's call
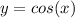 , so
, so
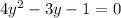
Where
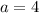 ,
,
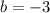 and
and
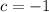 . Using the quadratic formula, we have
. Using the quadratic formula, we have
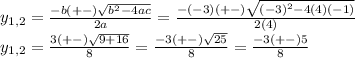
Where

But,
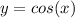
So,
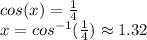 and
and
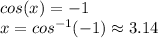
Therefore, the smallest radian solution is 3.14, approximately. And the next smallest radian solution is 1.32, approximately.