Question

Let S consist of the set of all distinct permutations of the letters of HIGHNOON. If a permutation is drawn at random from S, the probability that the two H's are not together can be written in simplest terms as ab. What is a+b?

Answer 1

7

Explanation:

HH I G NN OO

Total possibilities:

8!/(2!×2!×2!) = 5040

H together:

7!/(2!×2!) = 1260

H not together:

5040 - 1260 = 3780

Probability of H not together:

3780/5040

3/4

3 + 4 = 7

Answer 2

7

Explanation:

Let's first count how many ways we can order HIGHNOON without restrictions; this will be the denominator. There are 8 letters, so we have 8!. Then we divide this by 2! * 2! * 2! (the two H's, two N's, and two O's because we are overcounting otherwise):
`(8!)/(2!*2!*2!) =(8*7*6*5*4*3*2*1)/(2*2*2) =5040`.

Now, we want to find the number of ways the two H's are not together. But it's easier to do complementary counting, where we count the number of ways what we don't want to occur and subtract that from the total.

Let's put the two H's together like a big bundle and make it the one letter H (bold H to stand for two H's). Then, we are left with 7 "letters", so we have 7!. We still need to divide this by 2! * 2! (the two N's and two O's):
`(7!)/(2!*2!) =(7*6*5*4*3*2*1)/(2*2) =1260`.

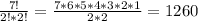Subtract this from 5040: 5040 - 1260 = 3780

So, our probability is 3780/5040 = 3/4. a + b = 7.

Hope this helps!