Question

A group consists of seven men and five women. Three people are selected to attend a conference.

a. In how many ways can three people be selected from this group of twelve?

b. In how many ways can three women be selected from the five women?

c. Find the probability that the selected group will consist of all women.

a. The number of ways to select three people from the group of twelve is 220

b. The number of ways to select three women from the group of five women is 0

Answer 1

a) 220

b) 10

c) 4.55% probability that the selected group will consist of all women.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

The order in which the people are selected is not important. So we use the combinations formula to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

a. In how many ways can three people be selected from this group of twelve?

`C_(12,3) = (12!)/(3!(12-3)!) = 220`

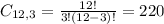
b. In how many ways can three women be selected from the five women?

Three women, from a set of 5. So

`C_(5,3) = (5!)/(3!(5-3)!) = 10`

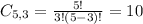
c. Find the probability that the selected group will consist of all women.

Desired outcomes:

3 women from a set of 4. So

`D = C_(5,3) = (5!)/(3!(5-3)!) = 10`

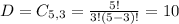
Total outcomes:

3 people, from a set of 12. So

`T = C_(12,3) = (12!)/(3!(12-3)!) = 220`

Probability:

`p = (D)/(T) = (10)/(220) = 0.0455`

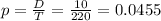
4.55% probability that the selected group will consist of all women.