Question

A hyperbola is represented using the equation (x-1)^2/4-(y+2)^2/16=1. What are the slopes of the asymptotes?

Answer 1

m=2

b=-4

Explanation:

Just did it on edg

Answer 2

the slope of the asymptotes are: 2 and -2

Explanation:

As we know the hyperbola equation is:

`((x-h)^2)/(b^2)-((y-k)^2)/(a^2)=1`

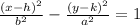
Given the hyperbola equation:

`((x-1)^(2) )/(4) - ((y+2)^(2) )/(16) = 1`

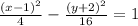
We have a=2 and b=4, h=1 and k=-2

and the asymptote equation of a translate hyperbola with equation is:

`y=\pm(b)/(a)(x-h)+k`

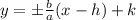
We substitute this values to get:

`y=\pm(4)/(2)(x-1) -2`

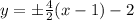
<=> y = 2x -4 or y = -2x

so the slope of the asymptotes are: 2 and -2