Question

A ladder 20 feet long leans against a building forming and angle of 46 degrees with the level ground. To the nearest foot how far away is the foot of the ladder to the building

Answer 1

The distance of the foot of the ladder to the building is 14 ft.

Explanation:

The length of ladder = 20 ft

Angle formed by ladder with level ground, θ = 46

We are required to find out the distance of the foot of the ladder from the building

The above question can be found out by using trigonometric relations as follows;

`Cos\theta = (Adjacent\, side \, to\, angle)/(Hypothenus\, side \, of\, triangle)`

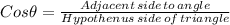
The adjacent side of the right triangle formed by the ladder the building and the ground is the distance of the foot of the ladder from the building

The hypotenuse side is the length of the ladder = 20 ft

Therefore;

Adjacent side of triangle = Hypotenuse × cosθ

∴ Distance of the foot of the ladder from the building = Hypotenuse × cosθ

Distance of the foot of the ladder from the building = 20 ft × cos(56)

Distance of the foot of the ladder from the building = 13.893 ft

To the nearest foot, the distance of the foot of the ladder to the building = 14 ft.